Sessions 6 et 7 :
Travaux pratiques

Sommaire du TP :

Présentation du TP

Le but de ce TP, qui fait l'objet de ces deux dernières sessions, est d'utiliser la programmation par contraintes pour résoudre les problèmes que vous avez modélisés sous la forme de CSPs lors de la deuxième session de cours.

Ce TP est composé des 5 exercices étudiés lors de la deuxième session. Pour chacun de ces exercices, nous commençons par vous rappeler l'énoncé du problème et sa modélisation sous la forme d'un CSP (X,D,C). Vous devez alors écrire le code Gnu-Prolog permettant de résoudre effectivement ce problème. Pour décrire les prédicats à écrire, on utilisera les conventions suivantes.

Exercice 1 : Retour de monnaie

1.1 - Description du problème

1.2 - Formalisation du problème sous la forme d'un CSP (X,D,C)

• X = {XE2, XE1, XC50, XC20, XC10}
  

  où XE2 désigne le nombre de pièces de 2 Euros à retourner, XE1 désigne le nombre de pièces de 1 Euro à retourner, ...

• Les domaines spécifient que la quantité de pièces retournées, pour un type de pièce donné, est comprise entre 0 et le nombre de pièces de ce type que l'on a en réserve :

  D(XE2) = {0,1,...,E2}
  D(XE1) = {0,1,...,E1}
  D(XC50) = {0,1,...,C50}
  D(XC20) = {0,1,...,C20}
  D(XC10) = {0,1,...,C10}

• Les contraintes spécifient que la somme à retourner doit être égale à la somme insérée moins le prix à payer :

  C = { 200*XE2 + 100*XE1 + 50*XC50 + 20*XC20 + 10*XC10 = T-P }

1.3 - Travail à faire

• Schéma d'appel :

  monnaie(+entier, +entier, +liste_de_5_termes, ?liste_de_5_termes)

• Description :

  monnaie(TotalDonné, TotalDu, Pièces_en_réserve, Pièces_à_retourner) réussit si
  

  • TotalDonné est la somme insérée dans le distributeur (en centimes d'euros),
  • TotalDu est la somme à payer (en centimes d'euros),
  • Pièces_en_réserve est la liste des quantités de pièces en réserve dans le distributeur,
  • Pièces_à_retourner s'unifie avec la liste des quantités de pièces à rendre par le distributeur.

• Exemple d'exécution de monnaie/4 :
  
  
  • Une première façon de faire (la plus simple à programmer) consiste à décider que les deux listes de pièces sont des listes d'entiers ordonnés en fonction des valeurs des pièces. Par exemple, on mettra toujours la quantité de pièces de 2 Euros en premier, puis celles de 1 Euro, puis celles de 50 centimes, 20 centimes et 10 centimes. Dans ce cas, un exemple d'exécution est :

    | ?- monnaie1(600,530,[5,7,4,3,5],L). L = [0,0,0,1,5] ? ; L = [0,0,0,2,3] ? ; L = [0,0,0,3,1] ? ; L = [0,0,1,0,2] ? ; L = [0,0,1,1,0] yes

    Cet exemple s'interprète de la façon suivante : la somme donnée est 600 centimes, alors que la somme à payer est 530 centimes ; le monnayeur a en stock 5 pièces de 2 Euros, 7 de 1 Euro, 4 de 50 centimes, 3 de 20 centimes et 5 de 10 centimes. Pour rendre la monnaie, on peut retourner 1 pièce de 20 centimes et 5 de 10, ou bien 2 pièces de 20 centimes et 3 de 10, ou bien ...
  
  
  • Une deuxième façon de faire, plus difficile à programmer mais plus explicite au moment de l'utilisation, consiste à décider que les deux listes de pièces sont des listes de couples de la forme X:Y où X donne la valeur des pièces (200, 100, 50, 20 ou 10), et Y donne la quantité de pièces de cette valeur. Dans ce cas, les listes n'ont plus besoin d'être ordonnées en fonction des valeurs des pièces. Un exemple d'exécution est :

    | ?- monnaie2(600,530,[100:7,200:5,10:5,50:4,20:3],L). L = [100:0,200:0,10:0,50:1,20:1] ? ; L = [100:0,200:0,10:1,50:0,20:3] ? ; L = [100:0,200:0,10:2,50:1,20:0] ? ; L = [100:0,200:0,10:3,50:0,20:2] ? ; L = [100:0,200:0,10:5,50:0,20:1] yes

Corrigé de l'exercice 1

Exercice 2 : Coloriage d'une carte

2.1 - Description du problème

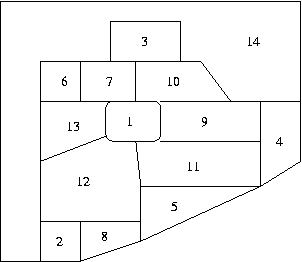
Il s'agit de colorier les 14 régions de la carte ci-dessous, de sorte que deux régions ayant une frontière en commun soient coloriées avec des couleurs différentes. On dispose pour cela des 4 couleurs suivantes : bleu, rouge, jaune et vert.

2.2 - Formalisation du problème sous la forme d'un CSP (X,D,C)

• X = {X1, X2, ..., X14}

  (On associe une variable Xi différente par région i à colorier.)

• pour tout Xi élément de X, D(Xi) = { bleu, rouge, vert, jaune }

  (Chaque région peut être coloriée avec une des 4 couleurs.)

• C = { Xi ≠ Xj / Xi et Xj sont 2 variables différentes de X et voisines(Xi,Xj) = vrai }

  où voisines/2 est un prédicat tel que voisines(X,Y) est vrai si X et Y sont deux régions voisines.

2.3 - Travail à faire

• Schéma d'appel :

  carte(?variable, +liste_d_options)

• Description :

  carte(L,O) réussit si
  

  • L s'unifie avec la liste des couleurs pour chacune des 14 régions, de la première à la dernière (les variables FD en Gnu-Prolog ne pouvant prendre que des variables entières, on remplacera les couleurs bleu, rouge, vert et jaune par les entiers 1, 2, 3 et 4).
  • O est la liste des options pour le prédicat fd_labeling/2 (voir le point 3 de la session 5 ou le manuel Gnu-Prolog). Ces options vous permettront de spécifier l'ordre d'affectation des variables.

• Exemple d'exécution de carte/2 : Pour chercher une solution au problème, sans heuristique particulière, on exécutera

  | ?- carte(A,[backtracks(B)]). A = [1,1,1,1,1,1,2,3,2,3,3,2,3,4] B = 4 ? yes

  La liste A indique qu'il faut colorier les régions 1 à 6 avec la couleur 1, les régions 7, 9 et 12 avec la couleur 2, les régions 8, 10, 11 et 13 avec la couleur 3 et la région 14 avec la couleur 4. Pour trouver cette première solution, Prolog a effectué 4 retours-arrières.

  Pour chercher une solution au problème en utilisant l'heuristique "échec d'abord", on exécutera

  | ?- carte(A,[variable_method(first_fail),backtracks(B)]). A = [1,1,1,1,1,1,2,3,2,3,3,2,3,4] B = 0 ? yes

  Prolog trouve la même solution... mais sans effectuer un seul retour-arrière.

  Pour chercher toutes les solutions au problème (sans les afficher), et compter le nombre total de retour-arrières effectués, on exécutera

  | ?- findall(B,carte(A,[backtracks(B)]),L), length(L,Nb_solutions), sum_list(L,Nb_backtracks). L = [4,1,1,1,...] Nb_solutions = 1968 Nb_backtracks = 3859 (10 ms) yes

  Dans ce cas, Prolog effectue 3859 retour-arrières pour calculer les 1968 solutions, sans utiliser d'heuristique.

  Pour chercher toutes les solutions au problème avec l'heuristique "échec d'abord", on exécutera

  | ?- findall(B,carte(A,[variable_method(first_fail),backtracks(B)]),L), length(L,Nb_solutions), sum_list(L,Nb_backtracks). L = [0,1,1,1,...] Nb_solutions = 1968 Nb_backtracks = 1967 (10 ms) yes

  Dans ce cas, Prolog effectue 1967 retour-arrières pour calculer les 1968 solutions...

Corrigé de l'exercice 2

---

Exercice 3 : Sel et moutarde

3.1 - Description du problème

On s'intéresse au problème suivant, posé initialement par Lewis Caroll :

Cinq amis, Barnabé, Casimir, Désiré, Ludovic et Martial, se retrouvent chaque jour au restaurant. Ils ont établi les règles suivantes, qu'ils appliquent chaque fois qu'on leur sert du boeuf :

• Barnabé prend du sel si et seulement si Casimir ne prend que du sel ou que de la moutarde. Il prend de la moutarde si et seulement si, ou bien Désiré ne prend ni sel ni moutarde, ou bien Martial prend les deux.
• Casimir prend du sel si et seulement si, ou bien Barnabé ne prend qu'un des deux condiments, ou bien Martial n'en prend aucun. Il prend de la moutarde si et seulement si Désiré ou Ludovic prennent les deux condiments.
• Désiré prend du sel si et seulement si ou bien Barnabé ne prend aucun condiment, ou bien Casimir prend les deux. Il prend de la moutarde si et seulement si Ludovic ou Martial ne prennent ni sel ni moutarde.
• Ludovic prend du sel si et seulement si Barnabé ou Désiré ne prennent ni sel ni moutarde. Il prend de la moutarde si et seulement si Casimir ou Martial ne prennent ni sel, ni moutarde.
• Martial prend du sel si et seulement si Barnabé ou Ludovic prennent des deux condiments. Il prend de la moutarde si et seulement si Casimir ou Désiré ne prennent qu'un seul condiment.

En fin de compte, que vont-ils mettre sur leurs steaks ?

3.2 - Formalisation du problème sous la forme d'un CSP (X,D,C)

• Variables :
  

  X = {xB, xC, xD, xL, xM}

• Domaines :
  

  pour toute variable xi de X, D(xi) = {rien, sel, moutarde, sel-et-moutarde}

• Contraintes :
  

  C = {C1,C2,C3,C4,C5,C6,C7,C8,C9,C10}
  avec

  • Barnabé prend du sel si et seulement si Casimir ne prend que du sel ou que de la moutarde.
    C1 = (xB=sel ou xB=sel-et-moutarde) <=> (xC=sel ou xC=moutarde) 
  • Il prend de la moutarde si et seulement si, ou bien Désiré ne prend ni sel ni moutarde, ou bien Martial prend les deux.
    C2 = (xB=moutarde ou xB=sel-et-moutarde) <=> (xD=rien xou xM=sel-et-moutarde) 
  • Casimir prend du sel si et seulement si, ou bien Barnabé ne prend qu'un des deux condiments, ou bien Martial n'en prend aucun.
    C3 = (xC=sel ou xC=sel-et-moutarde) <=> ((xB=sel ou xB=moutarde) xou xM=rien) 
  • Il prend de la moutarde si et seulement si Désiré ou Ludovic prennent les deux condiments.
    C4 = (xC=moutarde ou xC=sel-et-moutarde) <=> (xD=sel-et-moutarde ou xL=sel-et-moutarde) 
  • Désiré prend du sel si et seulement si ou bien Barnabé ne prend aucun condiment, ou bien Casimir prend les deux.
    C5 = (xD=sel ou xD=sel-et-moutarde) <=> (xB=rien xou xC=sel-et-moutarde) 
  • Il prend de la moutarde si et seulement si Ludovic ou Martial ne prennent ni sel ni moutarde.
    C6 = (xD=moutarde ou xD=sel-et-moutarde) <=> (xL=rien ou xM=rien)
  • Ludovic prend du sel si et seulement si Barnabé ou Désiré ne prennent ni sel ni moutarde.
    C7 = (xL=sel ou xL=sel-et-moutarde) <=> (xB=rien ou xD=rien)
  • Il prend de la moutarde si et seulement si Casimir ou Martial ne prennent ni sel, ni moutarde.
    C8 = (xL=moutarde ou xL=sel-et-moutarde) <=> (xC=rien ou xM=rien)
  • Martial prend du sel si et seulement si Barnabé ou Ludovic prennent des deux condiments.
    C9 = (xM=sel ou xM=sel-et-moutarde) <=> (xB=sel-et-moutarde ou xL=sel-et-moutarde)
  • Il prend de la moutarde si et seulement si Casimir ou Désiré ne prennent qu'un seul condiment
    C10 = (xM=moutarde ou xM=sel-et-moutarde) <=> (xC=sel ou xC=moutarde ou xD=sel ou xD=moutarde).
    

3.3 - Travail à faire

Ecrivez le prédicat sel_et_moutarde/1 suivant :


• Schéma d'appel :

  sel_et_moutarde(?liste_de_5_variables)

• Description :

  sel_et_moutarde([B,C,D,L,M]) réussit si B, C, D, L et M s'unifient respectivement avec ce que chacun des convives (respectivement Barnabé, Casimir, Désiré, Ludovic et Martial) doit mettre sur son steak. Les variables FD en Gnu-Prolog ne pouvant prendre que des valeurs entières, on remplacera les choix rien, sel, moutarde et sel_et_moutarde par les entiers 0, 1, 2 et 3 respectivement.

• Exemple d'exécution de sel_et_moutarde/1 :

  | ?- sel_et_moutarde(B, C, D, L, M). B = 1 C = 1 D = 2 L = 0 M = 2 ? ; no

  où, autrement dit, Barnabé et Casimir prennent du sel, Désiré et Martial prennent de la moutarde, et Ludovic ne prend rien. Notez que ce CSP n'admet qu'une seule solution.

Corrigé de l'exercice 3

---

Exercice 4 : Send more money

4.1 - Description du problème

On considère l'addition suivante :


   SEND
 + MORE
-------
= MONEY


où chaque lettre représente un chiffre différent (compris entre 0 et 9). On souhaite connaitre la valeur de chaque lettre, sachant que la première lettre de chaque mot représente un chiffre différent de 0.

4.2 - Formalisation du problème sous la forme d'un CSP (X,D,C)

• Variables : on associe une variable à chaque lettre

  X = {S,E,N,D,M,O,R,Y}

• Domaines : les variables correspondant au premier chiffre d'un mot (S et M) doivent prendre une valeur différente de 0 ; les autres peuvent prendre n'importe quelle valeur entre 0 et 9.

  D(S) = D(M) = {1,2,3,4,5,6,7,8,9}
  D(E) = D(N) = D(D) = D(O) = D(R) = D(Y) = {0,1,2,3,4,5,6,7,8,9}

• La contrainte exprime le fait que SEND+MORE=MONEY :

  C = { 1000*S + 100*E + 10*N + D
         +1000*M + 100*O + 10*R + E
          = 10000*M + 1000*O + 100*N + 10*E + Y}

4.3 - Travail à faire

Ecrivez le prédicat send/1 suivant :


• Schéma d'appel :

  send(?liste_de_8_variables)

• Description :

  send([S,E,N,D,M,O,R,Y]) réussit si SEND + MORE = MONEY.

• Exemple d'exécution de send/1 :

  | ?- send([S,E,N,D,M,O,R,Y]). D = 7 E = 5 M = 1 N = 6 O = 0 R = 8 S = 9 Y = 2 ? ; no

  où, autrement dit, 9567 + 1085 = 10652.

Corrigé de l'exercice 4

---

Exercice 5 : Le zèbre

5.1 - Description du problème

On s'intéresse au problème suivant, posé initialement par Lewis Caroll :

Cinq maisons consécutives, de couleurs différentes, sont habitées par des hommes de différentes nationalités. Chacun possède un animal différent, a une boisson préférée différente et fume des cigarettes différentes. De plus, on sait que :

1. Le norvégien habite la première maison,
2. La maison à coté de celle du norvégien est bleue,
3. L'habitant de la troisième maison boit du lait,
4. L'anglais habite la maison rouge,
5. L'habitant de la maison verte boit du café,
6. L'habitant de la maison jaune fume des kools,
7. La maison blanche se trouve juste après la verte,
8. L'espagnol a un chien,
9. L'ukrainien boit du thé,
10. Le japonais fume des cravens,
11. Le fumeur de old golds a un escargot,
12. Le fumeur de gitanes boit du vin,
13. Le voisin du fumeur de Chesterfields a un renard,
14. Le voisin du fumeur de kools a un cheval.

Qui boit de l'eau ? A qui appartient le zèbre ?


5.2 - Formalisation du problème sous la forme d'un CSP (X,D,C)

• Variables du problème: on associe une variable par attribut (couleur, animal, boisson, nationalité, cigarette)

  X = {blanche, rouge, verte, jaune, bleue, norvégien, anglais, ukrainien, japonais, espagnol, cheval, renard, zèbre, escargot, chien, thé, eau, lait, café, vin, kools, chesterfields, old_golds, cravens, gitanes}

• Domaines des variables:

  D(Xi) = {1,2,3,4,5}, pour toute variable Xi de X

• Contraintes:
  • On pose tout d'abord une contrainte pour chaque assertion de l'énoncé :

    norvégien = 1,
    bleue = norvégien + 1,
    lait = 3,
    anglais = rouge,
    verte = café,
    jaune = kools,
    blanche = verte + 1,
    espagnol = chien,
    ukrainien = thé,
    japonais = cravens,
    old_golds = escargot,
    gitanes = vin,
    (chesterfields = renard + 1) ou (chesterfields = renard - 1),
    (kools = cheval + 1) ou (kools = cheval - 1)
    

  • De plus, toutes les variables de même "type" doivent avoir des valeurs différentes (il ne peut pas y avoir plusieurs maisons qui ont la même couleur, ou un même animal, ...)

    blanche ≠ rouge ≠ verte ≠ jaune ≠ bleue,
    thé ≠ eau ≠ lait ≠ café ≠ vin,
    norvégien ≠ anglais ≠ ukrainien ≠ japonais ≠ espagnol,
    cheval ≠ renard ≠ zèbre ≠ escargot ≠ chien ≠ thé,
    kools ≠ chesterfields ≠ old_golds ≠ cravens ≠ gitanes

5.3 - Travail à faire

Ecrivez le prédicat zebre/1 suivant :


• Schéma d'appel :

  zebre(?variable)

• Description :

  zebre(L) réussit si L s'unifie avec une liste de couples attribut=valeur donnant la valeur de chacun des attributs (couleurs, nationalités, ...) du problème du zèbre.

• Exemple d'exécution de zebre/1 :

  | ?- zebre(L). L = [anglais=3, norvegien=1, espagnol=5, ukrainien=2, japonais=4,      bleu=2, rouge=3, vert=4, jaune=1, blanc=5,      cafe=4, the=2, eau=1, vin=5, lait=3,      kools=1, cravens=4, oldgolds=3, gitanes=5, chester=2,      chien=5, escargot=3, renard=1, cheval=2, zebre=4] ? ; no

  où, autrement dit, l'anglais est dans la troisième maison, le norvégien dans la première, l'espagnol dans la cinquième, ...

Corrigé de l'exercice 5