Session 3 :
Résolution de CSPs

Sommaire de la session 3 :

Présentation de la session

Ce qu'on va voir dans cette session...

Lors de la première session de cours, on a introduit le formalisme des CSPs, formalisme qui offre un cadre structurant pour modéliser des problèmes exprimés en termes de contraintes, et lors de la deuxième session vous vous êtes entrainés à modéliser des problèmes sous la forme de CSPs. On va maintenant étudier quelques algorithmes permettant de résoudre, de façon générique, certains de ces CSPs. On se restreindra aux CSPs sur les domaines finis, c'est-à-dire, les CSPs dont les domaines des variables sont des ensembles finis de valeurs. Le principe commun à tous les algorithmes que nous allons étudier est d'explorer méthodiquement l'ensemble des affectations possibles jusqu'à, soit trouver une solution (quand le CSP est consistant), soit démontrer qu'il n'existe pas de solution (quand le CSP est inconsistant).

...et ce qu'on ne verra pas (entre autres...)

• La résolution de problèmes d'optimisation sous contraintes

  Les algorithmes que nous allons étudier permettent de rechercher une solution à un CSP (n'importe laquelle, c'est-à-dire la première que l'on trouve). Suivant les applications, "résoudre un CSP" peut signifier autre chose que chercher simplement une solution. En particulier, il peut s'agir de chercher la "meilleure" solution selon un critère donné.

  Par exemple, pour le problème du coloriage d'une carte (exercice 2 de la session précédente), on peut chercher la solution qui utilise le moins de couleurs possibles ; pour le problème du retour de monnaie  (exercice 1 de la session précédente), on peut chercher la solution qui minimise le nombre total de pièces rendues, ...

  Ces problèmes d'optimisation sous contraintes, où l'on cherche à optimiser une fonction objectif donnée tout en satisfaisant toutes les contraintes, peuvent être résolus en explorant l'ensemble des affectations possibles selon la stratégie de "Séparation & Evaluation " ("Branch & Bound") bien connue en recherche opérationnelle. On n'étudiera pas cet algorithme dans ce cours.

• Les algorithmes de résolution de CSPs autres que sur les domaines finis

  Les algorithmes que nous allons étudier permettent de résoudre de façon générique n'importe quel CSP sur les domaines finis. Il existe d'autres algorithmes plus spécifiques qui tirent parti de connaissances sur les domaines et les types de contraintes pour résoudre des CSPs. Par exemple, les CSPs numériques linéaires sur les réels peuvent être résolus par l'algorithme du Simplex (bien connu en recherche opérationnelle) ; les CSPs numériques linéaires sur les entiers peuvent être résolus en combinant l'algorithme du Simplex avec une stratégie de "Séparation et Evaluation" ; les CSPs numériques non linéaires sur les réels peuvent être résolus en utilisant des techniques de propagation d'intervalles ; etc...

• Les algorithmes incomplets pour la résolution de CSPs
  

  Les algorithmes que nous allons étudier sont dits complets, dans le sens où l'on est certain de trouver une solution si le CSP est consistant. Cette propriété de complétude est fort intéressante dans la mesure où elle offre des garanties sur la qualité du résultat. En revanche, elle impose de parcourir exhaustivement l'ensemble des combinaisons possibles, et même si l'on utilise différentes techniques et heuristiques pour réduire la combinatoire, il existe certains problèmes pour lesquels ce genre d'algorithme ne termine pas "en un temps raisonnable". Par opposition, les algorithmes incomplets ne cherchent pas à envisager toutes les combinaisons, mais cherchent à trouver le plus vite possible une affectation "acceptable" : ces algorithmes permettent de trouver rapidement de bonnes affectations (qui violent peu ou pas de contraintes) ; en revanche, on n'est pas certain que la meilleure affectation trouvée par ces algorithmes soit effectivement optimale ; on est par ailleurs certain que l'on ne pourra pas prouver l'optimalité de l'affectation trouvée... Il existe différents algorithmes incomplets pour résoudre de façon générique des CSPs sur les domaines finis, généralement basés sur des techniques de recherche locale (éventuellement combinées avec des méthodes tabou, du recuit simulé, des algorithmes à base de fourmis...).

1 - L'algorithme "génère et teste"

1.1 - Principe de l'algorithme "génère et teste"

La façon la plus simple (et très naïve !) de résoudre un CSP sur les domaines finis consiste à énumérer toutes les affectations totales possibles jusqu'à en trouver une qui satisfasse toutes les contraintes. Ce principe est repris dans la fonction récursive "genereEtTeste(A,(X,D,C))" décrite ci-dessous. Dans cette fonction, A contient une affectation partielle et (X,D,C) décrit le CSP à résoudre (au premier appel de cette fonction, l'affectation partielle A sera vide). La fonction retourne vrai si on peut étendre l'affectation partielle A en une affectation totale consistante (une solution), et faux sinon.

1.2 - Exemple de trace d'exécution de "génère et teste"

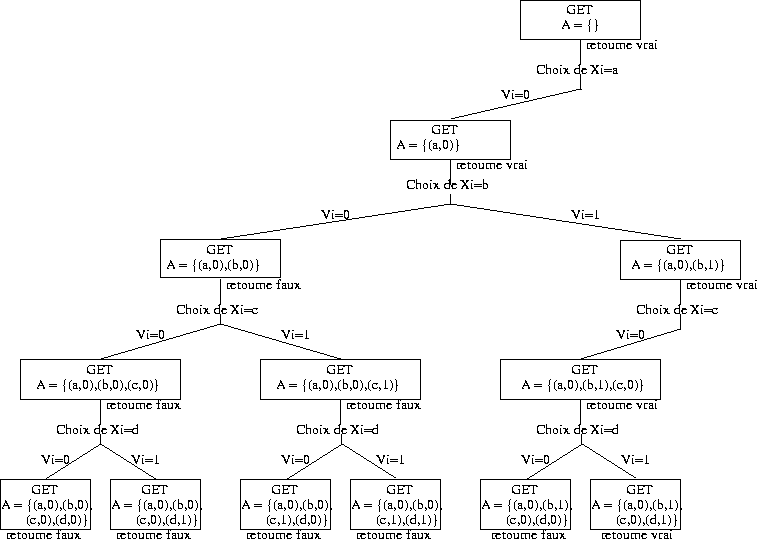
Considérons par exemple le CSP (X,D,C) suivant :

• X = {a,b,c,d}
• D(a) = D(b) = D(c) = D(d) = {0,1}
• C = { a ≠ b, c ≠ d, a+c < b }

2 - Critique de "génère et teste" et notion d'espace de recherche d'un CSP

L'algorithme "génère et teste" que nous venons de voir énumère l'ensemble des affectations complètes possibles, jusqu'à en trouver une qui soit consistante. L'ensemble des affectations complètes est appelé l'espace de recherche du CSP. Si le domaine de certaines variables contient une infinité de valeurs, alors cet espace de recherche est infini et on ne pourra pas énumérer ses éléments en un temps fini. Néanmoins, même en se limitant à des domaines comportant un nombre fini de valeurs, l'espace de recherche est souvent de taille tellement importante que l'algorithme "génère et teste" ne pourra se terminer en un temps "raisonnable". En effet, l'espace de recherche d'un CSP (X,D,C) comportant n variables ( X = {X1, X2, ..., Xn}) est défini par

E = { {(X1,v1), (X2,v2), ..., (Xn,vn)} / quelquesoit i compris entre 1 et n, vi est un élément de D(Xi) }

et le nombre d'éléments de cet espace de recherche est défini par

| E | = | D(X1) | * | D(X2) | * ... * | D(Xn) |

de sorte que, si tous les domaines des variables sont de la même taille k (autrement dit, | D(Xi) |=k), alors la taille de l'espace de recherche est

| E | = kⁿ

Ainsi, le nombre d'affectations à générer croit de façon exponentielle en fonction du nombre de variables du problème. Considérons plus précisément un CSP ayant n variables, chaque variable pouvant prendre 2 valeurs (k=2 ). Dans ce cas, le nombre d'affectations totales possibles pour ce CSP est 2ⁿ. En supposant qu'un ordinateur puisse générer et tester un milliard d'affectations par seconde (ce qui est une estimation vraiment très optimiste !), le tableau suivant donne une idée du temps qu'il faudrait pour énumérer et tester toutes les affectations en fonction du nombre de variables n.

Les améliorations de "génère et teste" que nous allons étudier dans la suite...

La conclusion de ce petit exercice de dénombrement est que, dès lors que le CSP a plus d'une trentaine de variables, on ne peut pas appliquer "bêtement" l'algorithme "génère et teste". Il faut donc chercher à réduire l'espace de recherche. Pour cela, on peut notamment :

• ne développer que les affectations partielles consistantes : dès lors qu'une affectation partielle est inconsistante, il est inutile de chercher à l'étendre en une affectation totale puisque celle-ci sera nécessairement inconsistante ;
  

  Cette idée est reprise dans l'algorithme "simple retour-arrière" que nous étudierons au point 3 de ce cours.
  

• réduire les tailles des domaines des variables en leur enlevant les valeurs "incompatibles" : pendant la génération d'affectations, on filtre le domaine des variables pour ne garder que les valeurs "localement consistantes" avec l'affectation en cours de construction, et dès lors que le domaine d'une variable devient vide, on arrête l'énumération pour cette affectation partielle ;
  

  Cette idée est reprise dans l'algorithme "anticipation" que nous étudierons au point 4 de ce cours.

• introduire des "heuristiques" pour "guider" la recherche : lorsqu'on énumère les affectations possibles, on peut essayer d'énumérer en premier celles qui sont les plus "prometteuses", en espérant ainsi tomber rapidement sur une solution.
  

  Cette idée est reprise dans le point 5 de ce cours.

... et celles que nous n'étudierons pas (entre autres...)

Il existe encore bien d'autres façons de (tenter de) réduire la combinatoire, afin de rendre l'exploration exhaustive de l'espace de recherche possible, que nous ne verrons pas dans ce cours. Par exemple, lors d'un échec, on peut essayer d'identifier la cause de l'échec (quelle est la variable qui viole une contrainte) pour ensuite "retourner en arrière" directement là où cette variable a été instanciée afin de remettre en cause plus rapidement la variable à l'origine de l'échec. C'est ce que l'on appelle le "retour arrière intelligent" ("intelligent backtracking").

Une autre approche particulièrement séduisante consiste à exploiter des connaissances sur les types de contraintes utilisées pour réduire l'espace de recherche.

considérons par exemple le CSP (X,D,C) suivant :

- X={a,b,c},
- D(a)=D(b)=D(c)={0,1,2,3,4, ..., 1000},
- C={4*a - 2*b = 6*c + 3}

L'espace de recherche de ce CSP comporte 1 milliard d'affectations ; pour résoudre ce CSP, on peut énumérer toutes ces combinaisons, en espérant en trouver une qui satisfasse la contrainte 4*a - 2*b = 6*c + 3... c'est long et si on remplace la borne supérieure 1000 par l'infini, ça devient carrément impossible. En revanche un simple raisonnement permet de conclure très rapidement que ce CSP n'a pas de solution : la partie gauche de l'équation "4*a - 2*b" donnera toujours un nombre pair, quelles que soient les valeurs affectées à a et b, tandis que la partie droite "6*c + 3" donnera toujours un nombre impair, quelle que soit la valeur affectée à c ; par conséquent, on ne peut trouver d'affectation qui satisfasse la contrainte, et il est inutile d'énumérer toutes les affectations possibles pour s'en convaincre !

Ce genre de raisonnement demande de l'intelligence, ou pour le moins des connaissances. De fait, l'homme est capable de résoudre des problèmes très combinatoires en raisonnant (en utilisant son "expérience" et des connaissances plus ou moins explicitées). Un exemple typique est le jeu d'échec : les grands joueurs d'échecs n'envisagent pour chaque coup à jouer que très peu de combinaisons (les meilleures évidemment !), éliminant par des raisonnements souvent difficiles à expliciter un très grand nombre de combinaisons moins intéressantes. Cela explique le fait que, malgré leur capacité à envisager un très grand nombre de combinaisons, les ordinateurs sont encore (bien souvent) moins forts que ces grands joueurs.

3 - L'algorithme "simple retour-arrière"

3.1 - Principe de l'algorithme "simple retour-arrière"

Par exemple, sur la trace d'exécution décrite en 1.2, on remarque que l'algorithme génère tous les prolongements de l'affectation partielle A={(a,0),(b,0)}, en énumérant toutes les possibilités d'affectation pour les variables c et d, alors qu'elle viole la contrainte a ≠ b. L'algorithme "simple retour-arrière" ne va donc pas chercher à étendre cette affectation, mais va "retourner en arrière" à l'affectation partielle précédente A={(a,0)}, et va l'étendre en affectant 1 à b , ...

Ce principe est repris dans la fonction récursive "simpleRetourArrière(A,(X,D,C))" décrite ci-dessous. Dans cette fonction, A contient une affectation partielle et (X,D,C) décrit le CSP à résoudre (au premier appel de cette fonction, l'affectation partielle A sera vide). La fonction retourne vrai si on peut étendre l'affectation partielle A en une affectation totale consistante (une solution), et faux sinon.

3.2 - Exemple de "trace d'exécution" de SimpleRetourArrière

Considérons le problème du placement de 4 reines sur un échiquier 4x4, et sa deuxième modélisation proposée au point 3 de la première session de cours :

• Variables : X = {X1,X2,X3,X4}
• Domaines : D(X1) = D(X2) = D(X3) = D(X4) = {1,2,3,4}
• Contraintes : C = {Xi ≠ Xj / i élément_de {1,2,3,4}, j élément_de {1,2,3,4} et i ≠ j}
                          U {Xi+i ≠ Xj+j / i élément_de {1,2,3,4}, j élément_de {1,2,3,4} et i ≠ j}
                          U {Xi-i ≠ Xj-j / i élément_de {1,2,3,4}, j élément_de {1,2,3,4} et i ≠ j}
  

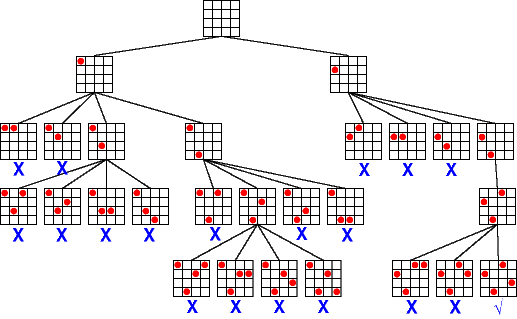Cette image est empruntée au "Guide to Constraint Programming" de Roman Bartak.

4 - L'algorithme "anticipation"

4.1 - Notions de filtrage et de consistance locale

Pour améliorer l'algorithme "simple retour-arrière", on peut tenter d'anticiper ("look ahead" en anglais) les conséquences de l'affectation partielle en cours de construction sur les domaines des variables qui ne sont pas encore affectées : si on se rend compte qu'une variable non affectée Xi n'a plus de valeur dans son domaine D(Xi) qui soit "localement consistante" avec l'affectation partielle en cours de construction, alors il n'est pas nécessaire de continuer à développer cette branche, et on peut tout de suite retourner en arrière pour explorer d'autres possibilités.

Pour mettre ce principe en oeuvre, on va, à chaque étape de la recherche, filtrer les domaines des variables non affectées en enlevant les valeurs "localement inconsistantes", c'est-à-dire celles dont on peut inférer qu'elles n'appartiendront à aucune solution. On peut effectuer différents filtrages, correspondant à différents niveaux de consistances locales, qui vont réduire plus ou moins les domaines des variables, mais qui prendront aussi plus ou moins de temps à s'exécuter : considérons un CSP (X,D,C), et une affectation partielle consistante A,

• le filtrage le plus simple consiste à anticiper d'une étape l'énumération : pour chaque variable Xi non affectée dans A, on enlève de D(Xi) toute valeur v telle que l'affectation A U {(Xi,v)} soit inconsistante.

  Par exemple pour le problème des 4 reines, après avoir instancié X1 à 1, on peut enlever du domaine de X2 la valeur 1 (qui viole la contrainte X1 ≠ X2) et la valeur 2 (qui viole la contrainte 1-X1 ≠ 2-X2).
  

  Un tel filtrage permet d'établir ce qu'on appelle la consistance de noeud, aussi appelée 1-consistance.
  (pour en savoir plus sur la consistance de noeud)

• un filtrage plus fort, mais aussi plus long à effectuer, consiste à anticiper de deux étapes l'énumération : pour chaque variable Xi non affectée dans A, on enlève de D(Xi) toute valeur v telle qu'il existe une variable Xj non affectée pour laquelle, pour toute valeur w de D(Xj), l'affectation A U {(Xi,v),(Xj,w)} soit inconsistante.

  Par exemple pour le problème des 4 reines, après avoir instancié X1 à 1, on peut enlever la valeur 3 du domaine de X2 car si X1=1 et X2=3, alors la variable X3 ne peut plus prendre de valeurs : si X3=1, on viole la contrainte X3 ≠ X1 ; si X3=2, on viole la contrainte X3+3 ≠ X2+2 ; si X3=3, on viole la contrainte X3 ≠ X2 ; et si X3=4, on viole la contrainte X3-3 ≠ X2-2.

  Notons que ce filtrage doit être répété jusqu'à ce plus aucun domaine ne puisse être réduit.
  Ce filtrage permet d'établir ce qu'on appelle la consistance d'arc, aussi appelée 2-consistance.
  (pour en savoir plus sur la consistance d'arc)

• un filtrage encore plus fort, mais aussi encore plus long à effectuer, consiste à anticiper de trois étapes l'énumération. Ce filtrage permet d'établir ce qu'on appelle la consistance de chemin, aussi appelée 3-consistance.

• ... et ainsi de suite... notons que s'il reste k variables à affecter, et si l'on anticipe de k étapes l'énumération pour établir la k-consistance, l'opération de filtrage revient à résoudre le CSP, c'est-à-dire que toutes les valeurs restant dans les domaines des variables après un tel filtrage appartiennent à une solution.

4.2 - Principe de l'algorithme "anticipation"

Le principe général de l'algorithme "anticipation" reprend celui de l'algorithme "simple retour-arrière", en ajoutant simplement une étape de filtrage à chaque fois qu'une valeur est affectée à une variable. Comme on vient de le voir au point 4.1, on peut effectuer différents filtrages plus ou moins forts, permettant d'établir différents niveaux de consistance locale (noeud, arc, chemin, ...). Par exemple, la fonction récursive "anticipation/noeud(A,(X,D,C))" décrite ci-dessous effectue un filtrage simple qui établit à chaque étape la consistance de noeud. Dans cette fonction, A contient une affectation partielle consistante et (X,D,C) décrit le CSP à résoudre (au premier appel de cette fonction, l'affectation partielle A sera vide). La fonction retourne vrai si on peut étendre l'affectation partielle A en une affectation totale consistante (une solution), et faux sinon.

4.3 - Exemple de "trace d'exécution" de "anticipation"

Considérons de nouveau le problème du placement de 4 reines sur un échiquier 4x4. L'enchainement des appels successifs à la fonction "Anticipation/noeud" peut être représenté par l'arbre suivant (les valeurs supprimées par le filtrage sont marquées d'une croix) :

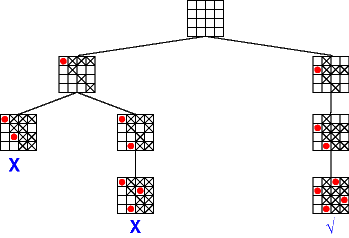Cette image est empruntée au "Guide to Constraint Programming" de Roman Bartak.

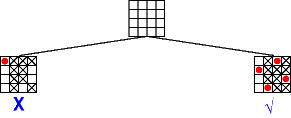Cette image est empruntée au "Guide to Constraint Programming" de Roman Bartak.

Ainsi, on constate sur le problème des 4 reines que le filtrage des domaines permet de réduire le nombre d'appels récursifs : on passe de 27 appels pour "simple retour-arrière" à 8 appels pour l'algorithme d'anticipation avec filtrage simple établissant une consistance de noeud. En utilisant des filtrages plus forts, comme celui qui établit la consistance d'arc, on peut encore réduire la combinatoire de 8 à 3 appels récursifs. Cependant, il faut noter que plus le filtrage utilisé est fort, plus cela prendra de temps pour l'exécuter...

De façon générale, on constate que, quel que soit le problème considéré, l'algorithme "anticipation/noeud" est généralement plus rapide que l'algorithme "simple retour-arrière" car le filtrage utilisé est vraiment peu coûteux. En revanche, si l'algorithme "anticipation/arc" envisage toujours moins de combinaisons que l'algorithme "anticipation/noeud", il peut parfois prendre plus de temps à l'exécution car le filtrage pour établir une consistance d'arc est plus long que celui pour établir la consistance de noeud.

5 - Intégration d'heuristiques

Les algorithmes que nous venons d'étudier choisissent, à chaque étape, la prochaine variable à instancier parmi l'ensemble des variables qui ne sont pas encore instanciées ; ensuite, une fois la variable choisie, ils essayent de l'instancier avec les différentes valeurs de son domaine. Ces algorithmes ne disent rien sur l'ordre dans lequel on doit instancier les variables, ni sur l'ordre dans lequel on doit affecter les valeurs aux variables. Ces deux ordres peuvent changer considérablement l'efficacité de ces algorithmes : imaginons qu'à chaque étape on dispose des conseils d'un "oracle-qui-sait-tout" qui nous dise quelle valeur choisir sans jamais se tromper ; dans ce cas, la solution serait trouvée sans jamais retourner en arrière... Malheureusement, le problème général de la satisfaction d'un CSP sur les domaines finis étant NP-complet, il est plus qu'improbable que cet oracle fiable à 100% puisse jamais être "programmé". En revanche, on peut intégrer des heuristiques pour déterminer l'ordre dans lequel les variables et les valeurs doivent être considérées : une heuristique est une règle non systématique (dans le sens où elle n'est pas fiable à 100%) qui nous donne des indications sur la direction à prendre dans l'arbre de recherche.

Les heuristiques concernant l'ordre d'instanciation des valeurs sont généralement dépendantes de l'application considérée et difficilement généralisables. En revanche, il existe de nombreuses heuristiques d'ordre d'instanciation des variables qui permettent bien souvent d'accélérer considérablement la recherche. L'idée générale consiste à instancier en premier les variables les plus "critiques", c'est-à-dire celles qui interviennent dans beaucoup de contraintes et/ou qui ne peuvent prendre que très peu de valeurs. L'ordre d'instanciation des variables peut être :

• statique, quand il est fixé avant de commencer la recherche ;
  
  
  Par exemple, on peut ordonner les variables en fonction du nombre de contraintes portant sur elles : l'idée est d'instancier en premier les variables les plus contraintes, c'est-à-dire celles qui participent au plus grand nombre de contraintes.
  
  
• ou dynamique, quand la prochaine variable à instancier est choisie dynamiquement à chaque étape de la recherche.
  
  
  Par exemple, l'heuristique "échec d'abord" ("first-fail" en anglais) consiste à choisir, à chaque étape, la variable dont le domaine a le plus petit nombre de valeurs localement consistantes avec l'affectation partielle en cours. Cette heuristique est généralement couplée avec l'algorithme "anticipation", qui filtre les domaines des variables à chaque étape de la recherche pour ne garder que les valeurs qui satisfont un certain niveau de consistance locale.